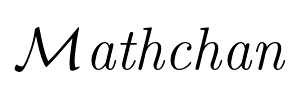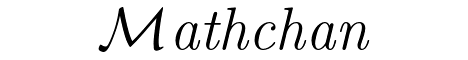Mathchan supports embedding
commutative diagrams:
Ab↓⏐CaB⏐↑cD
This can be done by using the
\begin{CD} ... \end{CD} environment in any of the above ways to to embed equations, or by specifying your code after starting a line with
,cd
.
If KaTeX's support is insufficient, diagrams can rendered using the
\tikzcd{...} command or by using the
\begin{tikzcd} ... \end{tikzcd} environment.
For example, pasting the following excerpt from the attached PDF (TikZ-CD manual):
\begin{tikzcd}[row sep=scriptsize, column sep=scriptsize]
& f^* E_V \arrow[dl] \arrow[rr] \arrow[dd] & & E_V \arrow[dl] \arrow[dd] \\
f^* E \arrow[rr, crossing over] \arrow[dd] & & E \\
& U \arrow[dl] \arrow[rr] & & V \arrow[dl] \\
M \arrow[rr] & & N \arrow[from=uu, crossing over]\\
\end{tikzcd}
Will render as the following figure on Mathchan:
The drawback is that you will have to pause typing and wait until the diagram renders while KaTeX can be displayed instantaneously.
It is recommended that you compile any LaTeX code yourself - or in Overleaf - before attempting to paste it on Mathchan.