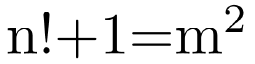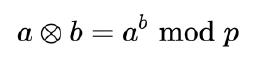
/math/ - Mathematics Catalog
| 25 Dec 2021 | Mathchan is launched into public |

Just by looking on a quarter of a circle with angle in it you know that:
By deriving everything we get:
And now it's easy to get
It is
Then you can compute
Similarily and even easier
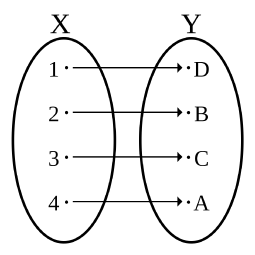
example of a real problem where complex numbers are used to derive a real solution?
Why are you not at the math room https://depvana.com/topic/202let's gather around mathematics there. As a start, I need examples of a real problem where complex numbers are used to derive a real solution?

https://users.math.yale.edu/mandelb
I can't attest if it's correct or not, but really I'm just posting this because I wanted it archived so that maybe some day someone will find value in it. Also you can do whatever you want with it, rewrite it or whatever.

There seems to be a whole community on Youtube that makes Mandelbrotzooms and seems to appreciate the psychedelic aesthetics and the relationship of these to PC hardware. Is this simply a continuation of the graphics demo scene?
I don't quite understand the appeal. However, I don't quite understand the math behind it either.

Topics:
-Propositional Calculus
-Methods of Proof
-Boolean Algebra and Circuits
-Sets, Relations and Functions
-Combinatorics
-Some more Counting Principles
-Partitions and Distributions

Methods of solving integrals
Primitive function of functionAntiderivative (aka indefinite integral) of a function
In a nutshell, integration is the opposite of differentiation:
Solving integrals in general is pretty hard, but there are a lot of established ways to do it. As OP I'll post some of the standard approaches, but this thread is about any kind of integration so feel free to post integrals and theirs solutions.
Most basic methods are:
- Using the table of integrals
- Using linearity property
- Using substitution
- Using partial integration
- Reducing quadratic to its cannonical form
- Partial decomposition

Spherical Harmonics
Hey /math/I've been trying to understand spherical harmonics to grok an ML paper that represented points in euclidean space in a rotation-and-translation-invariant way (https://arxiv.org/pdf/1802.08219.pd
Do you have any advice or perspectives on how to intuitively grasp what these harmonics are and mean, beyond just group theory definitions?

/math olympiad/ general
So, I have a cousin who wants to win medals in math competitions, especially IMO. Post resources, guides and tips for olympiads.his prep level: he's 12yo(7th standard), has completed mathematics books upto the 10th standard level. What should be his target next? And how do I help him clear doubts? We don't have decent teachers where we live, and the internet doesn't help much

Intuitionism and the Meaning of Truth after Gödel
I'm sorry if this belongs rather to the /phil/ section. I just want to discuss this topic and I guess, it has to do with math anyway.Some groups like the "New Atheits" and/or the so called "Intuitionists" (and the late Wittgenstein, too) think that you can make the following assumption:
"p is true" = "There is a proof for p [within a formal system]".
If it is impossible to provide a proof for p in principle, then you can claim that p is neither true nor false. Its just "undecidable".
My question is:
After the results of Tarski and Kurt Gödel, can we really still hold this assumption?
We see that "p is true" must be something different from "there is a proof for p" as there are some true statement of which the proof doesn't exist. We cannot define "truth" within a formal system and need some relation to something without the system itself. A semantic model.
In the light of this insights, the position that identified true with provability makes a lot less sense to me and many others.
Anyway, as far as I read, the critique of the inuitionists on the rule of double negation and the law of excluded middle relais a lot on the hidden premisse that "truth" and "can be proofen" is the same.
So, there viewpoint seems much less plausible anymore.
What do you think, anon?

>t. don't even remember high school math and only got the captcha right by chance, but i'm good at learning things
(Please refrain from "just use an engine"-type replies)

Self-studying category theory
(please move to /adv/ if this belongs there)I started with category theory a week ago with Lane's book. It's a bit hard and there are some examples (like lie groups) that I don't quite get. Related to this I've read Fraleigh's book on abstract algebra. Is this enough background or should I wait a bit before getting into category theory?
Thanks

Study plan general
Hello everyone. I have seen a lot of threads(book threads, IMO advice...) that seem to exist solely so people give advice and give comments on your study material.So I had an idea for a thread where we: state our goals, name the books(video series and other material) we plan to cover in a certain order, give an approximate deadline and other mathchan users can give suggestions, meaningful comments, advice and pointers to others!
I'll start:
My goal is to develop enough knowledge before I go to university where I hope to take advanced classes and spend more time on advanced topics while simultaneously getting myself ready for the national math competition(not my main focus, just for fun)
《Elementary math 1 i 2 notes》
-notes from my local university where they want to "bridge the gap between high-school and university math" (introductory logic, set theory, relations, functions, number theory, Euclidian geometry, vector spaces and analytic geometry)
《A Transition to Advanced Mathematics by Smith, Eggen, and St. Andre /// 101 problems in algebra》
-covers similair material as the already meantioned notes but in more detail
--------------I am here----------------
《Analysis I notes》
-notes from the local university, this time in calculus/analysis (what European universities call analysis is almost always just rigorous calculus or very elementary analysis since we cover calculus in HS)
《Linear Algebra Shilov》
《Šime Ungar, Analiza 3》
-same deal as before, rigorous calculus/ begginer analysis book for R^n
《101 problems in various topics, Andreescu books, generatingfunctionology, Problem solving strategies by Engels》
《Elements of Set Theory by Enderton》
《Introduction to Logic: and to the Methodology of Deductive Sciences by Alfred Tarski》
《An Introduction to the Theory of Numbers by Niven, Zuckerman, and Montgomery》
-mainly for competitive math but also as an introductory text
《The USSR olympiad problem book》
《Algebra by Artin》
《The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities by Steele》
-half for competitive maths, half since I heard analysis problems demand a lot of inequality knowledge
《Amann and Escher Analysis series》
-all three books
I hope to cover everything stated above in a 1.5-2 years. I covered the things above the "I'm here line" in three weeks while doing most of the exercises.

https://newsen.pku.edu.cn/PKUmedia/11888.html
https://newsen.pku.edu.cn/PKUmedia/>Of these 24 questions, Wei Dongyi completed 23 and a half, a record that even his coach was amazed by. He often solved all the questions in the first hour of the test. Many of the methods he used were self-invented and were much more concise than the standard processes, and became known as the "Wei Method".
>
In this competition, Wei beat the legendary Tao Zhexuan, who taught himself calculus at the age of seven and won the IMO gold medal at the age of 12, by a time ratio of 1:7. Tao Zhexuan was invited to solve the sixth problem of the finale, which took him seven hours, while Wei Dongyi took only one hour in the competition.
Is it really impossible to be like him with just learning and studying more? Is it really over, is only option actually suicide? Please be brutally honest, I don't want any false hope.(Even though I know the answer)
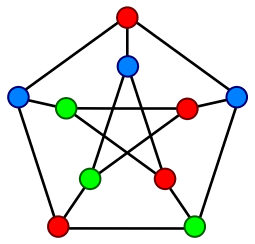
Roots of chromatic polynomials
Hey dudes, can you help me? I would like to reprove Alan Sokal's theorem in another way, I know how to calculate the roots of a chromatic polynomial, but there is a piece missing from my puzzle: how is n-degree a chromatic polynomial calculated?Pic's chromatic polynomial has degree 10 but it has three obviusly roots: 0,1,2; and it is not hard to calculate septic eq.

cool 2D function plots
Why are so few people interested in looking for nice function plots? It's like magic, a small formula of the x and y coordinate can make such a complex and beautiful picture. Can we start looking for such nice functions here? Use whatever tool you have (if you want I made a dirty JS tool at http://www.tastyfish.cz/functionplo
Fractional Distance: The Topology of the Real Number Line with Applications to the Riemann Hypothesis
>https://vixra.org/abs/2111.0072
Recent analysis has uncovered a broad swath of rarely considered real numbers called real numbers in the neighborhood of infinity. Here we extend the catalog of the rudimentary analytical properties of all real numbers by defining a set of fractional distance functions on the real number line and studying their behavior. The main results of are (1) to prove with modest axioms that some real numbers are greater than any natural number, (2) to develop a technique for taking a limit at infinity via the ordinary Cauchy definition reliant on the classical epsilon-delta formalism, and (3) to demonstrate an infinite number of non-trivial zeros of the Riemann zeta function in the neighborhood of infinity. We define numbers in the neighborhood of infinity as Cartesian products of Cauchy equivalence classes of rationals. We axiomatize the arithmetic of such numbers, prove all the operations are well-defined, and then make comparisons to the similar axioms of a complete ordered field. After developing the many underlying foundations, we present a basis for a topology.
Hmmm volumes?
Trying to look for a more mathemathical, vectorized summarized idea of Drawing correctly all the frames involved in the walk cycleFrom the idea that it is looping to maintaining constant balance between on step or cycle to another. But generally it needs to be summarized into a shape or curves or something easily read, mathemathically, that will tell where the pose go so to define the motion that is predetermined... which includes variety of things limping, running, crowling... assortments of so.
The prioritt idea is the balance and the repeat, so much less than abstract characteristic but rather the correct physics in accordance to the asked body motion

Listing all k-tuples!
Do you know of any interesting ways to list all possibleFirst you create a grid with two axes which you start numbering starting at 0. The square in the
We define
We can extend this to 3-tuples. But without using a 3-dimensional grid. We make a similar grid (right side of image), this time the upper axis is for the third element in the tuple and the left axis is just the sequence of 2-tuples I listed before for the 1st and 2nd elements of the 3-tuple.
Using that method, we get this for
A slightly less intuitive pattern...
Of course, you can generalize this method to get the formula:
I find this formula beautiful. Correct me in case you find mistakes!

History of infinite decimals
In his work which introduced decimals to Europe, Stevin wrote (converting it to modern notation) that when you divide 0.4 ÷ 0.03, the algorithm gives you infinitely many 3's. But he didn't call this infinite result an exact answer. Instead he noted 13.33⅓ and 13.333⅓ as exact answers while recommending instead truncating to 13.33 or however near the answer you require. So clearly the main idea of infinite decimals giving arbitrarily good approximations was there. But at what point did people start saying things like 0.4 ÷ 0.03 = 13.333... exactly?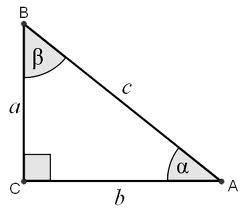
With respect to any of the two angles
Therefore, the complete set of trigonometric functions for the triangle in the pic related is:
Thus, just knowing the angle
And similarly, just knowing the angle
Intuition behind this is straightforward: For angles of a triangle, sine and cosine are bounded functions between zero and one.

The probability of kot id on /bant/
As well as "Jew" or "gay" id on /pol/. I mean it's a three-letter word where second letter can be written as a number (k0t) and first and last letter aren't the same.Now let's talk about IDs. They are 8-character sequences consisting of base64 characters (numbers, lowercase, uppercase letters, / and +). So, there can be
possible characters for one position in id and thus
possible IDs (BIG number :o).
Now back, to KOT.
You can write letters k, o and t in uppercase or lowercase and you can also write o as zero. That means you have
Suppose that first three letters of your ID is one of 12 possible K0Ts. We have 5 letters of ID left and they can be anything from base64 alphabet.
So, there are
So, it's also many, many ids. More than all cats, all humans, but less than all chickens in the world. So, maybe kot ID isn't really that rare.
Also there are 6 positions on which KoT id can happen:
KOTxxxxx
xKOTxxxx
xxKOTxxx
xxxKOTxx
xxxxKOTx
xxxxxKOT
We can assume that there are the same number of ids with KoT on n-th position where
Remember, that KOT id can happen twice, so we must exclude duplicates:
KOTKOTxx
KOTxKOTx
KOTxxKOT
xKOTKOTx
xKOTxKOT
xxKOTKOT
Each of these duplicate positions exists in
configurations.
Because one duplicate can belong to two sets of IDs with at least one kot id (KOTxxKOT can belong to KOTxxxxx and xxxxxKOT), our equation for number of all KOT ids must be:
Let's calculate it:
For every human on this planet there are approximately 10 KOT ids. :o
Now we can calculate probablility of having koT id:
Thus, k0t id happens approximately one time for every 3641 ids.
Now you can calculate daily probability, because I don't know if ids on /bant/ are boardwise or just one for every poster and thread. x)

therefore
and for k != 1
Now (You) choose random ball from any basket (every ball have the same probability of being chosen, not dependent on which basket is it placed in). You put new ball in a basket where this choosen ball was. :0 You repeat this t times.
In math language it is probably:
Now
The most bone-chilling, slow-burn, atmosphere-oozing thing I discovered about it:
HOLY SCIENCE!!!!!!!!1
Probability of having k balls after t time is always the same!!!!!
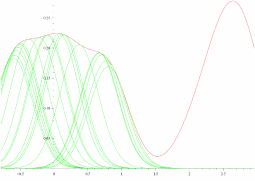
One Gaussian dominates another when I fit them in a natural way
The picture below shows (in red) a sum of Gaussian kernels with different means, but all having variance 1, i.e.f(x)=12π−−√∑i=1ne−12(x−μi)2 .
. The green curves show what I get if I select a point x0, and then "fit" a scaled Gaussian distribution g to f about x0, in the sense that I determine c and μ0 in the function
g(x):=c2π−−√e−12(x−μ0)2
so that g(x0)=f(x0) and g′(x0)=f′(x0). From numerical experimentation, it seems to always be the case that g(x)≤f(x) for all x. Does anyone know why this is so?
Prime factorization.
The brain dump of a managerie of often contracdictory and fantastic characters, from a mossad member turned professor, to an indian student turned part time street criminal, a homeless poet in philly, an ex-skin head, a former chinese investment banker, the owner of a multimillion dollar startup, two military veterans, and a cast of other folks.The result of a a simple discovery that a rich set of algebraic identities underlay the product of large primes.
For example, a series of variables related to n unknown value, d4, easily derived from known variables. d4a, d4u, d4z, d4H, etc.
Or c/d4, neither known by themselves, but the ratio of which is easily found, and the *product* of which, cd4, is the ratio of our product's factors, b/a.
Be warned the code is thick, mostly written by an indian guy, and translated by the rest of us over time. It is 198 pages of dense work, defining so many variables the original authors resorted to greek letters and elements from the periodic table for naming.
Good luck.
https://pastebin.com/Ad46Awcp
- Homework questions must be posted on /hr/ - Homework/Requests
- Career advice in mathematics belongs on /adv/ - Career Advice
- Testing Mathchan's markup should only be done on /test/ - Testing/Spamming
Equations can be embedded in multiple ways:
\eqn{...}or\math{...}command substitutions\[ ... \]
or\( ... \)
block substitutions$$ ... $$
or$ ... $
special block substitutions\begin{equation} ... \end{equation}or\begin{math} ... \end{math}environments- by starting a line with
,,
or,eqn
like one commonly would with >greentext.
Matrices can be embedded by using
\begin{matrix} ... \end{matrix} or \begin{array} ... \end{array} environments in any of the above ways to embed equations, or by starting a line with ,mat,
,pmat,
,smat
,bmat,
,Bmat,
,vmator
,Vmatand using
&and
\\symbols to delineate between columns and rows respectively.
Arrays can be embedded by using
\begin{array}{c|c:c} ... \end{array} environment in any of the above ways to embed equations, or by starting a line with ,arr{c|c:c} and using &and
\\symbols to delineate between columns and rows respectively. NOTE:
c|c:cis only one example of vertical separation (solid and dotted). Horizontal separation can be accomplished by using
\hlineor
\hdashlineafter
\\.
Alignments can be done by using
\begin{aligned} ... \end{aligned} in any of the above ways to embed equations, or by starting a line with ,alignand then using
\\symbols to start new lines and using
&symbol to specify how to align each line (usually, you want it attached to the equals sign, like
&=).`