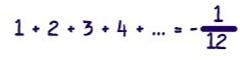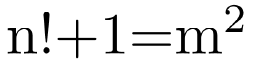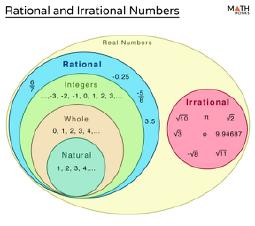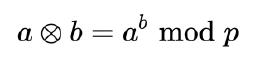
/math/ - Mathematics - Catalog

Name
Email
Subject	Preview Post
Comment
Preview
Verification	Instructions: Press the Get Captcha button to get a new captcha Find the correct answer and type the key in TYPE CAPTCHA HERE Press the Publish button to make a post Incorrect answer to the captcha will result in an immediate ban.
File
Password	(For file deletion.)


25 Dec 2021	Mathchan is launched into public

R: 14 / I: 2

If you solve the Brocard Problem, you IQ is at least 80.

What I said in the subject. It's so easy to prove. Search the problem and solve it, simple as that.

R: 5 / I: 1 I don't get it. Why are so many people in fractals nowadays?

There seems to be a whole community on Youtube that makes Mandelbrotzooms and seems to appreciate the psychedelic aesthetics and the relationship of these to PC hardware. Is this simply a continuation of the graphics demo scene?

I don't quite understand the appeal. However, I don't quite understand the math behind it either.

$Nov 12 23:55$

R: 1 / I: 0

Math help

I only know mathematics upto highschool only and that too barely and I want to learn mathematics from beginning rigorously. I need your help. Where should I start, where to begin. What books, what should I do and what should I not do

$Nov 12 23:49$

R: 1 / I: 0 Peak oil.

It's mathematically impossible for you to not die within a year.

I posted with the alias mustang on pol, you can see in archive.

$Nov 12 23:46$

R: 2 / I: 0

cubes

What do people make of these numbers?

$Nov 12 23:22$

R: 1 / I: 0

Can any given Probability be shown as Binary?

Can any given probability be reduced to a simple judgment, zero or one?
This would mean that we could reduce any distribution to the binomial distribution

$Nov 08 04:28$

R: 51 / I: 3 When did you realize that the reals are fake?
Mathematics can do without infinities.

$Oct 23 13:28$

R: 18 / I: 3

List of differential equations

Post diff eqs and their solutions.

$Oct 15 08:59$

R: 5 / I: 0

Solve these problems if you're not a retard

Solve these problems if you're not a retard:

Let

\langle a \rangle = (a_1, a_2, \ldots)

denote an infinite sequence of positive integers.

\rightarrow

Prove that there is no

\langle a \rangle

such that

\gcd(a_i + j, a_j + i) = 1

for all

i \neq j

.
Let

p \neq 2

be a prime.

\rightarrow

Prove that there is an

\langle a \rangle

such that

\gcd(a_i + j, a_j + i) = p

for all

i \neq j

.

$Oct 07 17:41$

R: 14 / I: 2

/book/s general thread

Request and deliver any books or book recommendation in this thread.

OP starts:
>Algebraic Topology, Allen Hatcher
https://pi.math.cornell.edu/~hatcher/AT/AT+.pdf
You really shouldn't go with any other book. Stick with Hatcher, even when you feel lost.

$Oct 05 13:34$

R: 5 / I: 0

Spherical Harmonics

Hey /math/

I've been trying to understand spherical harmonics to grok an ML paper that represented points in euclidean space in a rotation-and-translation-invariant way (https://arxiv.org/pdf/1802.08219.pdf). I found a great textbook on SO(3) (https://www.diva-portal.org/smash/get/diva2:1334832/FULLTEXT01.pdf), but while I can kind of maybe sort of follow what's being done with them in this particular paper I fail to really get an intuition of what spherical harmonics are, and it feels like there's some pretty beautiful insight in there.

Do you have any advice or perspectives on how to intuitively grasp what these harmonics are and mean, beyond just group theory definitions?

$Oct 05 07:16$

R: 59 / I: 7

/math olympiad/ general

So, I have a cousin who wants to win medals in math competitions, especially IMO. Post resources, guides and tips for olympiads.
his prep level: he's 12yo(7th standard), has completed mathematics books upto the 10th standard level. What should be his target next? And how do I help him clear doubts? We don't have decent teachers where we live, and the internet doesn't help much

$Sep 20 18:37$

R: 6 / I: 0

Dividing vectors

Any reason not to teach the algebra of Euclidean vectors like this? This would come after multiplication of vectors by scalars but before the scalar product of two vectors, and the target audience is students at the level of typical high school juniors or seniors.

$Sep 19 12:27$

R: 9 / I: 0 I know absolutely nothing about math, my knowledge is basically stuck to 7th grade stuff at best.
That said, even I can tell those wrong captcha answers are nonsensical, to the point I can easily get around verification by simply guessing the right answer.

Just a heads-up

$Sep 17 06:19$

R: 50 / I: 6 Is thrembo real? It's an integer between 6 and 7.

$Sep 16 22:47$

R: 1 / I: 0

Intuitionism and the Meaning of Truth after Gödel

I'm sorry if this belongs rather to the /phil/ section. I just want to discuss this topic and I guess, it has to do with math anyway.

Some groups like the "New Atheits" and/or the so called "Intuitionists" (and the late Wittgenstein, too) think that you can make the following assumption:
"p is true" = "There is a proof for p [within a formal system]".

If it is impossible to provide a proof for p in principle, then you can claim that p is neither true nor false. Its just "undecidable".

My question is:
After the results of Tarski and Kurt Gödel, can we really still hold this assumption?

We see that "p is true" must be something different from "there is a proof for p" as there are some true statement of which the proof doesn't exist. We cannot define "truth" within a formal system and need some relation to something without the system itself. A semantic model.
In the light of this insights, the position that identified true with provability makes a lot less sense to me and many others.

Anyway, as far as I read, the critique of the inuitionists on the rule of double negation and the law of excluded middle relais a lot on the hidden premisse that "truth" and "can be proofen" is the same.
So, there viewpoint seems much less plausible anymore.

What do you think, anon?

$Sep 16 22:46$

R: 0 / I: 0

Lindeberg‐Feller central limit theorem

What do you think, anon?
Made up Bullshit or genial insight?
Usufull or not?

$Sep 05 05:30$

R: 4 / I: 1

Hi

Im new.

$Aug 22 23:34$

R: 18 / I: 1 If you had a math exam and you could use your phone with internet while attempting the paper, what service would you use to solve questions?
Topics:
-Propositional Calculus
-Methods of Proof
-Boolean Algebra and Circuits
-Sets, Relations and Functions
-Combinatorics
-Some more Counting Principles
-Partitions and Distributions

$Aug 20 11:11$

R: 0 / I: 0 Are there any other people here who researched/studied zeta regularization (products)?

$Aug 19 22:15$

R: 1 / I: 1 I'm interested in making a game with simple 3D graphics (only consisting of simple shapes like cubes and pyramids) without using a 3D engine but I don't know the name of the specific math/geometry stuff I need to study in order to do that, can anyone orient me?
>t. don't even remember high school math and only got the captcha right by chance, but i'm good at learning things
(Please refrain from "just use an engine"-type replies)

$Aug 18 04:09$

R: 2 / I: 0

JEE ADVANCE/ISI

Topics which are not in high school syllabus but might help in JEE Maths or Physics questions.

Book recommendations or advice for JEE Maths or Physics

$Aug 14 07:05$

R: 14 / I: 6

Self-studying category theory

(please move to /adv/ if this belongs there)

I started with category theory a week ago with Lane's book. It's a bit hard and there are some examples (like lie groups) that I don't quite get. Related to this I've read Fraleigh's book on abstract algebra. Is this enough background or should I wait a bit before getting into category theory?

Thanks

$Aug 08 11:52$

R: 5 / I: 0

Study plan general

Hello everyone. I have seen a lot of threads(book threads, IMO advice...) that seem to exist solely so people give advice and give comments on your study material.
So I had an idea for a thread where we: state our goals, name the books(video series and other material) we plan to cover in a certain order, give an approximate deadline and other mathchan users can give suggestions, meaningful comments, advice and pointers to others!
I'll start:
My goal is to develop enough knowledge before I go to university where I hope to take advanced classes and spend more time on advanced topics while simultaneously getting myself ready for the national math competition(not my main focus, just for fun)
《Elementary math 1 i 2 notes》
-notes from my local university where they want to "bridge the gap between high-school and university math" (introductory logic, set theory, relations, functions, number theory, Euclidian geometry, vector spaces and analytic geometry)

《A Transition to Advanced Mathematics by Smith, Eggen, and St. Andre /// 101 problems in algebra》
-covers similair material as the already meantioned notes but in more detail

--------------I am here----------------

《Analysis I notes》
-notes from the local university, this time in calculus/analysis (what European universities call analysis is almost always just rigorous calculus or very elementary analysis since we cover calculus in HS)

《Linear Algebra Shilov》

《Šime Ungar, Analiza 3》
-same deal as before, rigorous calculus/ begginer analysis book for R^n

《101 problems in various topics, Andreescu books, generatingfunctionology, Problem solving strategies by Engels》

《Elements of Set Theory by Enderton》

《Introduction to Logic: and to the Methodology of Deductive Sciences by Alfred Tarski》

《An Introduction to the Theory of Numbers by Niven, Zuckerman, and Montgomery》
-mainly for competitive math but also as an introductory text

《The USSR olympiad problem book》

《Algebra by Artin》

《The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities by Steele》
-half for competitive maths, half since I heard analysis problems demand a lot of inequality knowledge

《Amann and Escher Analysis series》
-all three books

I hope to cover everything stated above in a 1.5-2 years. I covered the things above the "I'm here line" in three weeks while doing most of the exercises.

$Aug 08 11:35$

R: 36 / I: 4

Name the blurry books

Please name all the books in picrel. Also review the curriculum shown. Are the books shown in the picrel enough to cover the mentioned topics. If so how long would it take.

$Aug 06 21:57$

R: 13 / I: 2

/mg/ - maths general "altchan edition"

Talk maths.

$Jul 20 07:41$

R: 8 / I: 2

Entrance Exam

You can solve this, right?

$Jul 19 11:51$

R: 4 / I: 1

This week I am reading

This is a thread to post a paper or book you are reading currently.

$Jul 19 07:44$

R: 4 / I: 0 do you look like a scientist?

$Jul 05 05:43$

R: 24 / I: 3

https://newsen.pku.edu.cn/PKUmedia/11888.html

https://newsen.pku.edu.cn/PKUmedia/11888.html

>Of these 24 questions, Wei Dongyi completed 23 and a half, a record that even his coach was amazed by. He often solved all the questions in the first hour of the test. Many of the methods he used were self-invented and were much more concise than the standard processes, and became known as the "Wei Method".

>
In this competition, Wei beat the legendary Tao Zhexuan, who taught himself calculus at the age of seven and won the IMO gold medal at the age of 12, by a time ratio of 1:7. Tao Zhexuan was invited to solve the sixth problem of the finale, which took him seven hours, while Wei Dongyi took only one hour in the competition.

Is it really impossible to be like him with just learning and studying more? Is it really over, is only option actually suicide? Please be brutally honest, I don't want any false hope.(Even though I know the answer)

$Jul 01 05:40$

R: 13 / I: 2 -1/12

contradiction or too complex for mere mortals to understand?

$Jul 01 05:37$

R: 3 / I: 2 Mathematically speaking, what is the optimal strategy for yahtzee?

$Jun 24 17:58$

R: 2 / I: 1 https://arxiv.org/abs/2405.03599

https://www.youtube.com/watch?v=1emC3ncjblU

https://people.mpim-bonn.mpg.de/gaitsgde/GLC/

$Jun 13 18:32$

R: 0 / I: 0

$ a \otimes x = b $ mod p

The discrete logarithm

a^x=b

mod p is polynomial with a,p prime ≠ 2; the question is if a=2 or a is a dialed number is still polynomial? I troved a way, but is a class of solutions.

$May 18 09:12$

R: 11 / I: 5

$Apr 15 16:48$

R: 16 / I: 0 no eureka for today, gentlemen

$Apr 14 10:31$

R: 1 / I: 0 Evaluate

You should be able to solve this

$Apr 08 09:18$

R: 13 / I: 1 What the fuck is a Polynomial and how do I solve one?

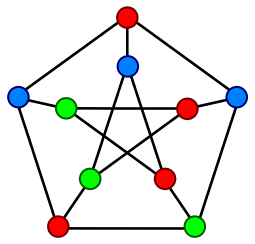
$Mar 15 13:40$

R: 0 / I: 0

Roots of chromatic polynomials

Hey dudes, can you help me? I would like to reprove Alan Sokal's theorem in another way, I know how to calculate the roots of a chromatic polynomial, but there is a piece missing from my puzzle: how is n-degree a chromatic polynomial calculated?
Pic's chromatic polynomial has degree 10 but it has three obviusly roots: 0,1,2; and it is not hard to calculate septic eq.

$Mar 01 15:45$

R: 0 / I: 0

Can you solve this?

What do you guys think about competitive national exams like CSAT, Gaokao, JEE and more?

$Feb 25 12:25$

R: 10 / I: 3 what's the most important trig concept you remember?

$Feb 13 05:51$

R: 10 / I: 1 What the hell is a quotient group and why should i care? it's just a bunch of cosets

$Feb 03 23:13$

R: 2 / I: 1

cool 2D function plots

Why are so few people interested in looking for nice function plots? It's like magic, a small formula of the x and y coordinate can make such a complex and beautiful picture. Can we start looking for such nice functions here? Use whatever tool you have (if you want I made a dirty JS tool at http://www.tastyfish.cz/functionplot.html).

$Jan 14 08:43$

R: 14 / I: 7

Number Theory

What's the deal with local and global fields?

$Dec 31 03:41$

R: 2 / I: 1 Talk schemes

$Dec 30 17:01$

R: 9 / I: 0 >Bijection
>Isomorphism
>Equivalence Relation
It's all just the same, innit?

$Dec 28 22:07$

R: 2 / I: 1

/Neumann General/ Birthday

Happy Birthday von Neumann

$Dec 27 10:46$

R: 0 / I: 0

Jungius' Logica Hamburgensis?

hat is your opinion about the Logica Hamburgensis, anon?

What do you say about?
https://www.digitale-sammlungen.de/de/view/bsb11273280?page=7

$Dec 05 04:35$

R: 12 / I: 2 Prove you are not a Midwit.

$Nov 08 18:30$

R: 2 / I: 0

Euclids elements

Has anyone read euclids elements or has ability to elucidate upon this geometry

$Nov 05 01:16$

R: 0 / I: 0 >There is no Eulerian path along the bridges of Konigsberg?
>What if we dropped a 5000 kg bomb on the city?

$Nov 03 20:49$

R: 6 / I: 0 He is right about everything.

$Oct 22 17:17$

R: 3 / I: 0 Hodge conjecture is true. How do you prove it?

$Oct 18 21:26$

R: 5 / I: 2 The Riemann hypothesis is false. I have a few independent negations by direct counterexample and they are presented in papers with varying degrees of rigor. In this "quick" proof, I present a fully rigorous proof upon an unproven proposition. Obvioulsy, this fails to negate RH due to the unproven proposition but it concisely states the method I use. In a longer paper, I do it without that proposition's assumption and in a *much* longer paper I start with Euclid's Elements, assume nothing else, and then show that RH is consequently false. That paper is linked below and if I can post the PDF, I will post it.

Fractional Distance: The Topology of the Real Number Line with Applications to the Riemann Hypothesis
>https://vixra.org/abs/2111.0072
Recent analysis has uncovered a broad swath of rarely considered real numbers called real numbers in the neighborhood of infinity. Here we extend the catalog of the rudimentary analytical properties of all real numbers by defining a set of fractional distance functions on the real number line and studying their behavior. The main results of are (1) to prove with modest axioms that some real numbers are greater than any natural number, (2) to develop a technique for taking a limit at infinity via the ordinary Cauchy definition reliant on the classical epsilon-delta formalism, and (3) to demonstrate an infinite number of non-trivial zeros of the Riemann zeta function in the neighborhood of infinity. We define numbers in the neighborhood of infinity as Cartesian products of Cauchy equivalence classes of rationals. We axiomatize the arithmetic of such numbers, prove all the operations are well-defined, and then make comparisons to the similar axioms of a complete ordered field. After developing the many underlying foundations, we present a basis for a topology.

$Sep 29 21:43$

R: 1 / I: 0

Hmmm volumes?

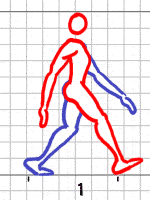
Trying to look for a more mathemathical, vectorized summarized idea of Drawing correctly all the frames involved in the walk cycle

From the idea that it is looping to maintaining constant balance between on step or cycle to another. But generally it needs to be summarized into a shape or curves or something easily read, mathemathically, that will tell where the pose go so to define the motion that is predetermined... which includes variety of things limping, running, crowling... assortments of so.

The prioritt idea is the balance and the repeat, so much less than abstract characteristic but rather the correct physics in accordance to the asked body motion

$Aug 28 11:51$

R: 3 / I: 0

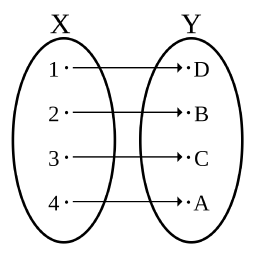
Listing all k-tuples!

Do you know of any interesting ways to list all possible

k

-tuples of nonnegative integers in order? Or in other words, do you know a function

f(n)

such that for every

(a, b)

with integers

a, b \ge 0

, there exists an

n \ge 0

with

f(n) = (a, b)

? Well, I do! I'll be showing my way.

First you create a grid with two axes which you start numbering starting at 0. The square in the

p

th row and

q

th column will have the tuple

(p - 1, q - 1) = (a, b)

. Not

(n, m)

because we start at 0. Now, we draw a line that connects the squares like in the left grid of the image attached (translucent, red line). The line creates this one-dimensional sequence of 2-tuples:

(0, 0) \rightarrow (0, 1) \rightarrow (1, 0) \rightarrow (2, 0) \rightarrow (1, 1) \rightarrow (0, 2) \rightarrow (0, 3) \rightarrow (1, 2) \rightarrow (2, 1) \rightarrow (3, 0) \rightarrow (4, 0) \rightarrow \dots

You should notice the pattern. Like that, I've listed all 2-tuples.

We define

f_k(n)

as our function that maps

\lbrace 0, 1, 2, \ldots \rbrace

to the set of all

k

-tuples of nonnegative integers.

We can extend this to 3-tuples. But without using a 3-dimensional grid. We make a similar grid (right side of image), this time the upper axis is for the third element in the tuple and the left axis is just the sequence of 2-tuples I listed before for the 1st and 2nd elements of the 3-tuple.

Using that method, we get this for

k = 3

:

f_3(0) = (0, 0, 0)\\ f_3(1) = (0, 0, 1)\\ f_3(2) = (0, 1, 0)\\ f_3(3) = (1, 0, 0)\\ f_3(4) = (0, 1, 1)\\ f_3(5) = (0, 0, 2)\\ \ \ \ \vdots

A slightly less intuitive pattern...

Of course, you can generalize this method to get the formula:

f_{k+1}(n) = f_k(b(n)) \cup s(n)

. The union symbol is used here to append

s(n)

to to the

k

-tuple

f_k(b(n))

.

b(n)

refers to the first element of

f_2(n)

and

s(n)

refers to the second. Also, it isn't particularly hard to prove that these functions indeed do return every possible tuple.

I find this formula beautiful. Correct me in case you find mistakes!

$Aug 20 18:47$

R: 4 / I: 1

History of infinite decimals

In his work which introduced decimals to Europe, Stevin wrote (converting it to modern notation) that when you divide 0.4 ÷ 0.03, the algorithm gives you infinitely many 3's. But he didn't call this infinite result an exact answer. Instead he noted 13.33⅓ and 13.333⅓ as exact answers while recommending instead truncating to 13.33 or however near the answer you require. So clearly the main idea of infinite decimals giving arbitrarily good approximations was there. But at what point did people start saying things like 0.4 ÷ 0.03 = 13.333... exactly?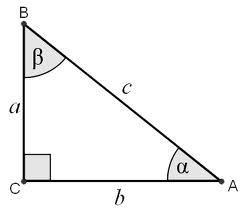

$Aug 14 17:50$

R: 3 / I: 0 The sum of the coefficients of the expanded Sum of the n first postive integer powers seem to equal the denominator.
Seems pretty cool and I can't find anything about it online

$Aug 10 15:09$

R: 7 / I: 0

Methods of solving integrals

Primitive function of function

f(x)

over some interval

x\in[a, b]

is a function

F(x)

whose derivative is the function

f(x)

on that interval.

\qquad \forall x\in[a, b],\quad F'(x) = f(x)

Antiderivative (aka indefinite integral) of a function

f(x)

is a family of its primitive functions which differ by a constant

C\in\mathbb{R}

:

\qquad \int f(x)\mathrm{d}x = F(x) + C

In a nutshell, integration is the opposite of differentiation:

\qquad \frac{\mathrm{d}\int f(x)\mathrm{d}x}{\mathrm{d}x} = F(x)

\qquad \mathrm{d}\int f(x)\mathrm{d}x = f(x)\mathrm{d}x

\qquad \int\mathrm{d}F(x) = F(x) + C

Solving integrals in general is pretty hard, but there are a lot of established ways to do it. As OP I'll post some of the standard approaches, but this thread is about any kind of integration so feel free to post integrals and theirs solutions.

Most basic methods are:

Using the table of integrals
Using linearity property
Using substitution
Using partial integration
Reducing quadratic to its cannonical form
Partial decomposition

$Jul 19 17:18$

R: 13 / I: 0 How to solve an equation?

$May 04 06:40$

R: 0 / I: 0

Merkoba Calculator

This is a multi-line calculator I made.
Each line is associated with a variable.
You can reference variables in other lines.
It uses math.js at 64 precision.
Allows normal and fraction mode.
http://calculator.merkoba.com/

$Apr 14 10:43$

R: 5 / I: 0 What's the difference between Trigometric Anaylsis and Calculus? especially as it pertains to vectors pic somewhat related

$Jan 19 12:10$

R: 3 / I: 0 Let

g(X)

be the minimal poly of

\gamma

. Then we have

\mathbb{Z}[X]/\langle g(X) \rangle \cong \mathbb{Z}[\gamma]

So then we can see that

\mathbb{Z}[\gamma]/\langle p \rangle \cong \mathbb{Z}[X] / \langle g(X), p \rangle

My question: is this a general rule of rings that given a homomorphism

\phi : R/I \rightarrow S

with ker

\phi = J

, then

R/(I + J) \cong S/J

?

$Jan 14 17:09$

R: 5 / I: 1

Continuous vs Discrete: The Great Debate

I've tried writing longform posts but don't get much traction. Let's try a shortform post.

$Sep 04 21:57$

R: 12 / I: 2 Trigonometric functions are used to relate the angles of a right triangle to its sides.

\qquad \sin(\text{angle}) = \frac{\text{opposite}}{\text{hypotenuse}}\quad\cos(\text{angle}) =\frac{\text{adjacent}}{\text{hypotenuse}}\quad\tan(\text{angle}) = \frac{\sin(\text{angle})}{\cos(\text{angle})} = \frac{\text{opposite}}{\text{adjacent}}\quad

With respect to any of the two angles

\alpha

or

\beta

(the third angle of a right triangle is, of course,

90^\text{o}

thereofre it's irrelevant) three sides can be identified with the following names: hypotenuse, opposite and adjacent. The hypotenuse is easy to identify and it's the longest i.e.

c

. The adjacent side is the one that's "touching" the angle; for angle

\alpha

that would be

b

, while for angle

\beta

that would be

a

. The opposite side is the one that's NOT "touching" the angle; for angle

\alpha

that would be

a

, while for angle

\beta

that would be

b

.

Therefore, the complete set of trigonometric functions for the triangle in the pic related is:

\qquad \sin(\alpha) = \frac{a}{c}\quad \cos(\alpha) = \frac{b}{c}\quad \tan(\alpha) = \frac{a}{b}

\qquad \sin(\beta) = \frac{b}{c}\quad \cos(\beta) = \frac{a}{c}\quad \tan(\beta) = \frac{b}{a}

Thus, just knowing the angle

\alpha

allows conversion of any side to any other side:

	$a$	$b$	$c$
$a=$	$a$	$b\tan(\alpha)$	$c\sin(\alpha)$
$b=$	$\frac{a}{\tan(\alpha)}$	$b$	$c\cos(\alpha)$
$c=$	$\frac{a}{\sin(\alpha)}$	$\frac{b}{\cos(\alpha)}$	$c$

And similarly, just knowing the angle

\beta

also allows conversion of any side to any other side:

	$a$	$b$	$c$
$a=$	$a$	$\frac{b}{\tan(\beta)}$	$c\cos(\beta)$
$b=$	$a\tan(\beta)$	$b$	$c\sin(\beta)$
$c=$	$\frac{a}{\cos(\beta)}$	$\frac{b}{\sin(\beta)}$	$c$

Intuition behind this is straightforward: For angles of a triangle, sine and cosine are bounded functions between zero and one.

(0 \leq \sin(x)\leq 1,\; 0\leq \cos(x) \leq1)

. Multiplying something with these functions should produce a smaller or equal value, while dividing something with these functions should produce a larger or equal value. Since hypotenuse is the longest, multiplying it with sine or cosine will "reduce" it to a leg. Similarly, dividing a leg by sine or cosine will "grow" it into a hypotenuse. A leg can be converted to another leg by "growing" it into a hypotenuse first, then "reducing" it to another leg which effectively is the same as multiplying the leg with a tangent value of the angle that the leg opposes.

$Sep 02 12:29$

R: 7 / I: 0

The probability of kot id on /bant/

As well as "Jew" or "gay" id on /pol/. I mean it's a three-letter word where second letter can be written as a number (k0t) and first and last letter aren't the same.

Now let's talk about IDs. They are 8-character sequences consisting of base64 characters (numbers, lowercase, uppercase letters, / and +). So, there can be

10 + 26 + 26 + 2 = 64

possible characters for one position in id and thus

K_0 = 64^8 = 2^{48} = 281\ 474\ 976\ 710\ 656

possible IDs (BIG number :o).

Now back, to KOT.
You can write letters k, o and t in uppercase or lowercase and you can also write o as zero. That means you have

2\times3\times2 = 12

combinations of base64 characters that can make up the word "k0T".

Suppose that first three letters of your ID is one of 12 possible K0Ts. We have 5 letters of ID left and they can be anything from base64 alphabet.
So, there are

K_1 = 12 \times 64^5 = 12 \times 2^{30} = 12\ 884\ 901\ 888

So, it's also many, many ids. More than all cats, all humans, but less than all chickens in the world. So, maybe kot ID isn't really that rare.

Also there are 6 positions on which KoT id can happen:
KOTxxxxx
xKOTxxxx
xxKOTxxx
xxxKOTxx
xxxxKOTx
xxxxxKOT

We can assume that there are the same number of ids with KoT on n-th position where

n = 1 ... 6

.

Remember, that KOT id can happen twice, so we must exclude duplicates:
KOTKOTxx
KOTxKOTx
KOTxxKOT
xKOTKOTx
xKOTxKOT
xxKOTKOT

Each of these duplicate positions exists in

K_2 = 12 \times 12 \times 64^2 = 144 \times 2^{12} = 589824

configurations.

Because one duplicate can belong to two sets of IDs with at least one kot id (KOTxxKOT can belong to KOTxxxxx and xxxxxKOT), our equation for number of all KOT ids must be:

6 \times K_1 - 6 \times K_2

Let's calculate it:

6 \times K_1 - 6 \times K_2 =

6 \times 12 \times 2^{30} - 6 \times 144 \times 2^{12} =

72 \times 2^{30} - 864 \times 2^{12} =

77\ 305\ 872\ 384

For every human on this planet there are approximately 10 KOT ids. :o

Now we can calculate probablility of having koT id:

\frac{77305872384}{K_0} = \frac{77305872384}{281474976710656} \approx 0.00027464563 \approx \frac{1}{3641}

Thus, k0t id happens approximately one time for every 3641 ids.
Now you can calculate daily probability, because I don't know if ids on /bant/ are boardwise or just one for every poster and thread. x)

$Aug 28 13:11$

R: 10 / I: 0 Supose you have two baskets with one ball each. Probability that one basket has k ball in 0-th time is

p_{0,k}

therefore

p_{0,1} = 1

and for k != 1

p_{0,k} = 0

.

Now (You) choose random ball from any basket (every ball have the same probability of being chosen, not dependent on which basket is it placed in). You put new ball in a basket where this choosen ball was. :0 You repeat this t times.

In math language it is probably:

p_{t,k} = p_{t-1,k-1}\frac{k-1}{t+1} + p_{t-1,k}\frac{t-k}{t+1}

Now

The most bone-chilling, slow-burn, atmosphere-oozing thing I discovered about it:

p_{t,k} = \frac{1}{t+1}

HOLY SCIENCE!!!!!!!!1

Probability of having k balls after t time is always the same!!!!!

$Jul 25 04:36$

R: 3 / I: 0 What are some good books to learn symplectic geometry with?

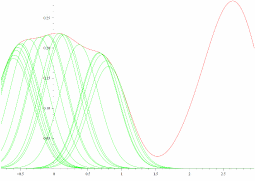
$Jul 18 09:58$

R: 0 / I: 0

One Gaussian dominates another when I fit them in a natural way

The picture below shows (in red) a sum of Gaussian kernels with different means, but all having variance 1, i.e.
f(x)=12π−−√∑i=1ne−12(x−μi)2 .
. The green curves show what I get if I select a point x0, and then "fit" a scaled Gaussian distribution g to f about x0, in the sense that I determine c and μ0 in the function
g(x):=c2π−−√e−12(x−μ0)2
so that g(x0)=f(x0) and g′(x0)=f′(x0). From numerical experimentation, it seems to always be the case that g(x)≤f(x) for all x. Does anyone know why this is so?

$May 20 11:56$

R: 0 / I: 0 Are there mathemathics i can use to fix the silhouette of this image? like the back tip of the helmet?
to make it look "correct"?

$May 05 15:53$

R: 4 / I: 1

lambda calculus

does anyone have good resources to learn the notation? i could figure out basic things like

((λ x . x) (λ a . a))

but got filtered by

(((λ f . (λ x . (f x))) (λ a . a)) (λ b . b))

$May 03 15:39$

R: 3 / I: 2 how do i start learning advanced math, ahead of my classes? any good textbooks/sources? what is your advice?

$Apr 01 09:59$

R: 4 / I: 0

Prime factorization.

The brain dump of a managerie of often contracdictory and fantastic characters, from a mossad member turned professor, to an indian student turned part time street criminal, a homeless poet in philly, an ex-skin head, a former chinese investment banker, the owner of a multimillion dollar startup, two military veterans, and a cast of other folks.

The result of a a simple discovery that a rich set of algebraic identities underlay the product of large primes.

For example, a series of variables related to n unknown value, d4, easily derived from known variables. d4a, d4u, d4z, d4H, etc.
Or c/d4, neither known by themselves, but the ratio of which is easily found, and the *product* of which, cd4, is the ratio of our product's factors, b/a.

Be warned the code is thick, mostly written by an indian guy, and translated by the rest of us over time. It is 198 pages of dense work, defining so many variables the original authors resorted to greek letters and elements from the periodic table for naming.

Good luck.

https://pastebin.com/Ad46Awcp

$Jan 24 21:48$

R: 3 / I: 1 What the heck is a Euclid distance? Why is it different from the Minsk distance and Cosine distance?
If i have a matrix as so, i'm expected to make all three distance matrices from it

X = \begin{bmatrix} 0 & 2 \\ 2 & 0 \\ 3 & 1 \\ 5 & 1 \end{bmatrix}

Also this probably has something to do with statistics idk

$Jan 01 04:23$

R: 1 / I: 1 (sticky) This board is for the discussion of mathematics.

Homework questions must be posted on /hr/ - Homework/Requests
Career advice in mathematics belongs on /adv/ - Career Advice
Testing Mathchan's markup should only be done on /test/ - Testing/Spamming

Equations can be embedded in multiple ways:

```
\eqn{...}
```
or
```
\math{...}
```
command substitutions
```
\[ ... \]
```
or
```
$ ... $
```
block substitutions
```
$$ ... $$
```
or
```
$ ... $
```
special block substitutions

\begin{equation} ... \end{equation}

or

\begin{math} ... \end{math}

environments

by starting a line with
```
,,
```
or
```
,eqn
```
like one commonly would with >greentext.

Matrices can be embedded by using

\begin{matrix} ... \end{matrix}

or

\begin{array} ... \end{array}

environments in any of the above ways to embed equations, or by starting a line with

,mat

,

,pmat

,

,smat

,bmat

,

,Bmat

,

,vmat

or

,Vmat

and using

and

\\

symbols to delineate between columns and rows respectively.

Arrays can be embedded by using

\begin{array}{c|c:c} ... \end{array}

environment in any of the above ways to embed equations, or by starting a line with

,arr{c|c:c}

and using

and

\\

symbols to delineate between columns and rows respectively. NOTE:

c|c:c

is only one example of vertical separation (solid and dotted). Horizontal separation can be accomplished by using

\hline

or

\hdashline

after

\\

.

Alignments can be done by using

\begin{aligned} ... \end{aligned}

in any of the above ways to embed equations, or by starting a line with

,align

and then using

\\

symbols to start new lines and using

symbol to specify how to align each line (usually, you want it attached to the equals sign, like

&=

).`